+44 330 818 7254Short Communication - International Research Journal of Engineering Science, Technology and Innovation ( 2024) Volume 10, Issue 1
Received: 08-Apr-2024, Manuscript No. irjesti-24-132487; Editor assigned: 11-Apr-2024, Pre QC No. irjesti-24-132487 (PQ); Reviewed: 25-Apr-2024, QC No. irjesti-24-132487; Revised: 01-May-2024, Manuscript No. irjesti-24-132487 (R); Published: 29-May-2024, DOI: 10.14303/2315-5663.2024.117
This paper is intended to build a connection between dynamics and fluid mechanics. Since Lagrangian equations are very useful tools in dynamics now it is discovered that it can be also used in fluid mechanics, so connection can be built through this equation. Here, the lagrangian equation is derived from the momentum equation in fluid mechanics, and then the equation is applied to three different coordinates, Cartesian, cylindrical and spherical. Certainly the application of the equation is not limited to these three different coordinates. This is just for illustration. Many applications are expected.
Lagrangian equation; Dynamics; Fluid mechanics; Tools
Fluid mechanics is my major in my graduate study. In my memory when I started to study the fluid mechanics, I learned a complete set of different equations in fluid mechanics. It seems not much related with dynamics. Here I hope that I can get some connections between dynamics and fluid mechanics. In dynamics, Lagrangian equations are very useful tools; many equations are developed with the use of Lagrangian equation. Now based on the momentum equation in fluid mechanics, I derived the Lagrangian equation, so I prove that Lagrangian equation can be also used in fluid mechanics. To simplify the derivation, I started the derivation for incompressible fluid, so a more general form of Lagrangian equation can be further developed. To illustrate the use of the equation, some examples are given. Those are especially in very familiar area, so people can immediately recognize that the equation is working. Momentum equations for inviscid incompressible fluid in Cartesian, cylindrical and spherical coordinates are chosen for the illustration (Figures 1 and 2) [1-4].
Derivation of Lagrangian equation
In dynamics, especially in the Chapter of Lagrange’s equations, the position vector r is considered as a function of generalized coordinates qi and time t.
r=r (qi, t)
And elocity r is a f nction of generali ed coordinates qi, generalized velocity ̇ and time t.
ṙ= ṙ (qi,q i̇,t)
These notations will be used here in this paper.
In fluid mechanics, for incompressible fluid, when a portion of fluid is observed, following this portion of fluid, the momentum equation can be written as:
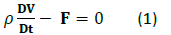
Where ρ is density,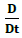
is the substantial derivative, V is
velocity and F is force per volume.
Applying the virtual work concept, the equation becomes:
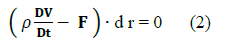
Since the virtual work is done at one instant of time, r is function of generalized coordinates only, so
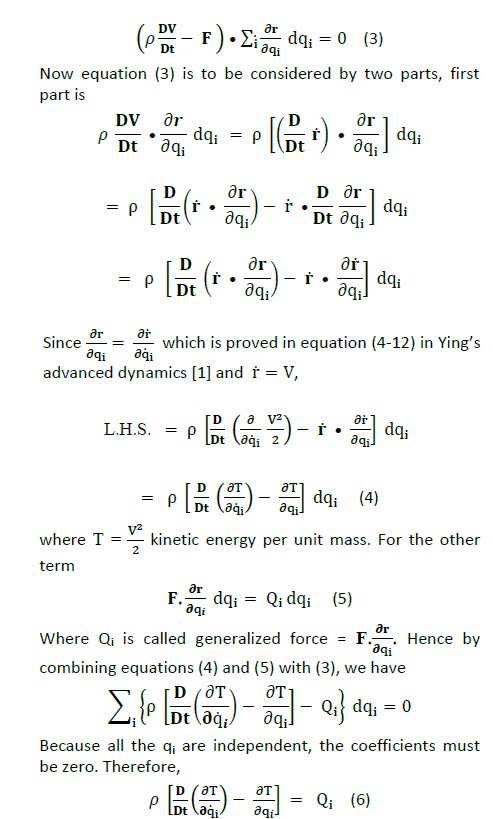
This is the Lagrangian equation for incompressible fluid in fluid mechanics.
Application
To illustrate the use of the equation three different coordinates are chosen, Cartesian, cylindrical and spherical. Since they are familiar to everybody, they can be recognized easily.
Cartesian coordinates
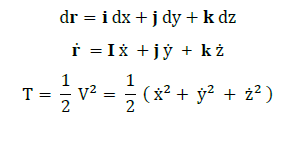
Applying the Lagrangian equation
Figure 1. Cylindrical coordinates.
Figure 2. Spherical coordinates.
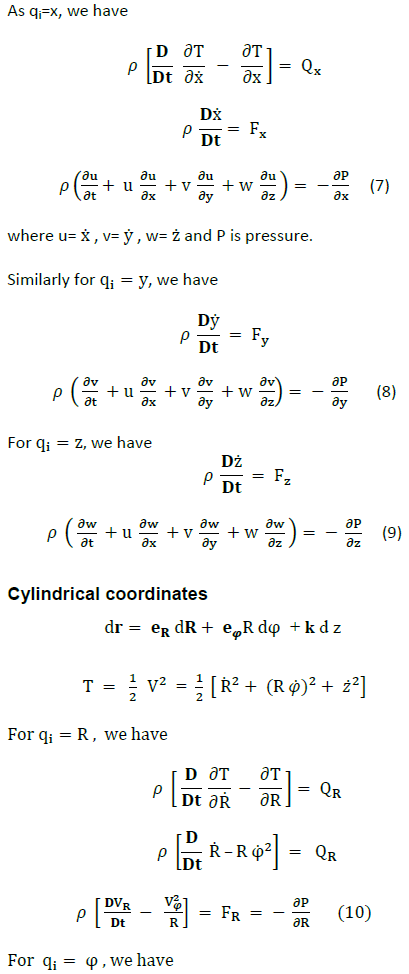
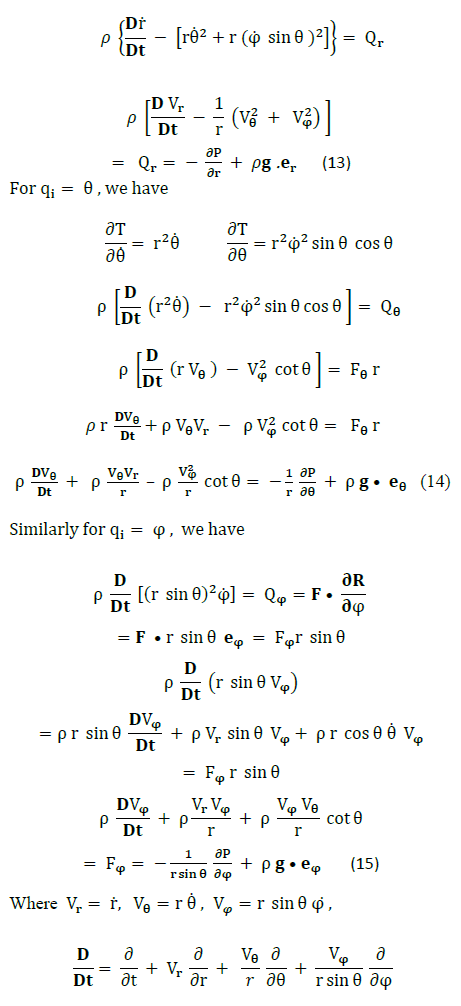
This paper may be considered as the first step for the use of Lagrangian equation in fluid mechanics. An inviscid incompressible fluid is considered here, more general form of the Lagrangian equation can be developed for more general kind of fluid. Now the door is open, further development and application of the equation can be very fruitful to scientists in fluid mechanics.